Os valores da variável, ordenados por ordem crescente, são:

x₁=2  ;  x₂=3  ;  x₃=4  ;  x₄=5  e  x₅=6

O valor x₁ ocorre 5 vezes, então a frequência absoluta deste valor é 5, isto é,       =5

 

Sendo        o número de vezes que ocorre         , procedendo às contagens, tem-se:

n₁=5  ;  n₂=9  ;  n₃=5  ;  n₄=4  e  n₅=2

 

Repara que:

n₁+n₂+n₃+n₄+n₅=N

e que:

5+9+5+4+2=25

 

No caso geral, se a variável assume k valores distintos, tem-se:

 

 

 

Com a frequência relativa do valor         é dada por                          determinando-se a frequência relativa de cada um dos valores.

Por exemplo, 

 

Para se obter o valor em percentagem, basta multiplicar            por 100 , pelo que o valor de f₁, em percentagem, é 20% (0,2 x 100) .

 

Este tipo de informação pode ser organizada numa tabela de frequências como a que se segue:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Na 1ª coluna da tabela apresentam-se os valores da variável, por ordem crescente, no caso desta ser quantitativa discreta. Na 2ª coluna indica-se o número de vezes que cada um dos valores da variável ocorre (frequência absoluta). Na 3ª  coluna calculam-se as frequências relativas, podendo ser apresentadas em fração, número decimal ou percentagem.

 

A análise da informação a partir da tabela de frequências permite concluir imediatamente que:

 

• 36% dos apartamentos têm três habitantes ;

• apenas dois apartamentos são habitados por seis pessoas.

 

Repara que a soma das frequências relativas, quando representadas em fração ou número decimal, é igual a 1. No caso destas estarem representadas em percentagem a soma é igual a 100%.

 

No caso geral, se a variável assume k valores distintos, tem - se 

 

 

EXERCÍCIO/EXEMPLO

 

O diretor de turma reúne regularmente com os encarregados de educação para lhes dar informações, entre as quais a relacionada com a assiduidade dos alunos.

No final do 1º período, o diretor de turma fez o levantamento das faltas dadas pelos alunos, obtendo os seguintes dados:

 

2 0 2 5 0 1 3

4 0 1 4 0 4 1

0 0 0 3 2 1 1 

1 2 0 1 5 3 2

 

Pretende-se organizar a informação de modo a identificar facilmente a resposta a questões do tipo:

 

i) Quantos alunos deram exatamente quatro faltas ?

ii) Quantos alunos deram menos de quatro faltas ?

iii) Qual é a percentagem de alunos em que o número de faltas não excedeu três?

 

RESOLUÇÃO:

 

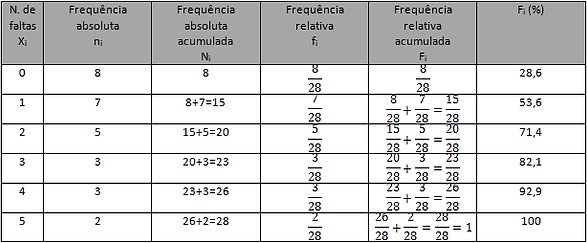
Uma possível organização consiste em construir uma tabela de frequências absolutas e relativas como se indica a seguir.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Em relação à questão i), por observação da tabela, conclui - se, de forma imediata, que três alunos deram exatamente quatro faltas.

Para responder à questão ii) é necessário somar o número de alunos que deram zero faltas, uma falta, duas faltas e três faltas

 

n₁ + n₂ + n₃ + n₄ = 8 + 7 + 5 + 6 = 23

 

Portanto, 23 alunos deram menos de quatro faltas.

 

Para responder à questão iii) é necessário acumular as frequências relativas, obtendo-se

 

 

 

 

como                    , conclui-se, aproximadamente 82,1% dos alunos não excederam três faltas.

A obtenção das respostas às questões ii) e iii) não foi por simples observação da tabela como se pretendia. Houve necessidade de acumular as frequências absolutas no caso da questão ii) e as frequências relativas no caso da questão iii)

Esta dificuldade pode ser ultrapassada se acrescentarmos à tabela mais duas colunas correspondentes às chamadas frequencias acumuladas.

 

Sendo,                                                                                            , tem-se:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Para responder às questões ii) e iii) basta observar a tabela.

ii) Quantos alunos deram menos de quatro faltas ?

A resposta corresponde ao valor 23.

iii) Qual é a percentagem de alunos em que o número de faltas não excedeu três?

A resposta corresponde ao valor 82,1%

 

No caso geral, tem-se:

 

 

 

 

 

 

 

 

 

 

 

 

Esta informação pode ser representada através de uma função F, função cumulativa, que a cada x, variável independente, faz corresponder a frequência absoluta acumulada do maior valor da variável estatistica que não excede x.

 

No caso geral, num estudo estatistico em que a variável torna os valores                                         , com frequências absolutas acumuladas                                          , chama-se função cumulativa F à função assim definida: 

 

 

 

 

 

 

Repare que o dominio da função cumulativa é IR e o contradominio é o conjunto                                        .

De igual forma se define função cumulativa para as frequências relativas acumuladas. Essa função designa-se por F* e tem dominio IR e contradominio o conjunto                                         . O contradominio toma valores pertencentes ao intervalo [0,1].